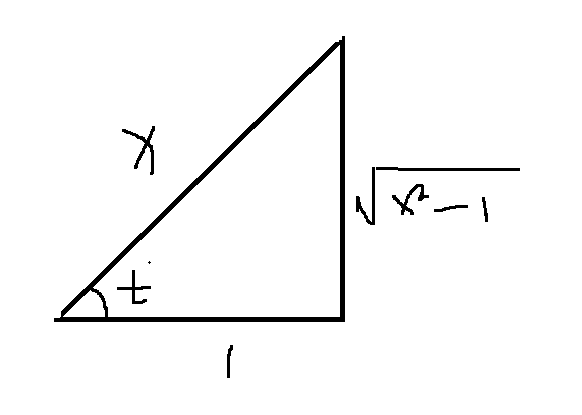微分方程通解公式
微分方程中的l n x lnx l n x
一阶微分方程
齐次y ′ + p ( x ) y = 0 y^{'}+p(x)y=0 y ′ + p ( x ) y = 0
C e − ∫ p ( x ) d x Ce^{-\int p(x)dx}
C e − ∫ p ( x ) d x
非齐次y ′ + p ( x ) y = q ( x ) y^{'}+p(x)y=q(x) y ′ + p ( x ) y = q ( x )
e − ∫ p ( x ) d x [ ∫ q ( x ) e ∫ p ( x ) d x d x + C ] e^{-\int p(x)dx}[\int q(x)e^{\int p(x)dx}dx + C]
e − ∫ p ( x ) d x [ ∫ q ( x ) e ∫ p ( x ) d x d x + C ]
二阶微分方程
齐次y ′ ′ + p ( x ) y ′ + q ( x ) y = 0 y^{''}+p(x)y^{'}+q(x)y=0 y ′ ′ + p ( x ) y ′ + q ( x ) y = 0
特征方程r1!=r2
C 1 e r 1 x + C 2 e r 2 x C_1e^{r_1x}+C_2e^{r_2x}
C 1 e r 1 x + C 2 e r 2 x
特征方程r1=r2=r
( C 1 + C 2 x ) e r x (C_1+C_2x)e^{rx}
( C 1 + C 2 x ) e r x
特征方程α ± i β \alpha \pm i \beta α ± i β
e a x ( c 1 cos β x + c 2 sin β x ) e^{ax}(c_1\cos\beta x+c_2\sin\beta x)
e a x ( c 1 cos β x + c 2 sin β x )
非齐次y ′ ′ + p ( x ) y ′ + q ( x ) y = f ( x ) y^{''}+p(x)y^{'}+q(x)y=f(x) y ′ ′ + p ( x ) y ′ + q ( x ) y = f ( x )
求解非齐次方程,需要求出其对应齐次方程的通解Y Y Y y ∗ y^* y ∗
q ( x ) q(x) q ( x ) P n ( x ) P_n(x) P n ( x )
特征方程解的形式
设特解形式
0不是特征方程的根
R n x R_nx R n x
0是特征方程的单根
x R n x xR_nx x R n x
0是特征方程的重根
x 2 R n x x^2R_nx x 2 R n x
q(x)形式P n ( x ) e a x P_n(x)e^{ax} P n ( x ) e a x
特征方程解的形式
设特解形式
α \alpha α e α x R n x e^{\alpha x}R_nx e α x R n x
α \alpha α x e α x R n x xe^{\alpha x}R_nx x e α x R n x
α \alpha α x 2 e α x R n x x^2e^{\alpha x}R_nx x 2 e α x R n x
q ( x ) q(x) q ( x ) e α x ( a cos β x + b sin β x ) e^{\alpha x}(a\cos\beta x+b\sin\beta x) e α x ( a cos β x + b sin β x )
特征方程解的形式
设特解形式
α ± i β \alpha\pm i\beta α ± i β e α x ( A cos β x + B sin β x ) e^{\alpha x}(A\cos\beta x+B\sin\beta x) e α x ( A cos β x + B sin β x )
α ± i β \alpha\pm i\beta α ± i β x e α x ( A cos β x + B sin β x ) xe^{\alpha x}(A\cos\beta x+B\sin\beta x) x e α x ( A cos β x + B sin β x )
奇偶函数的判别公式
奇偶函数的加减乘除
参与计算的函数
结果
奇函数± \pm ±
非奇非偶函数
奇函数± \pm ±
奇函数
偶函数± \pm ±
偶函数
奇函数× / \times/ × /
奇函数
奇函数× / \times/ × /
偶函数
偶函数× / \times/ × /
偶函数
奇偶函数的判别技巧
参与计算的函数
结果
奇函数的奇数次方
奇函数
奇函数的偶数次方
偶函数
偶函数的奇数次方
偶函数
偶函数的偶数次方
偶函数
无穷级数
等比级数
∑ n = 0 ∞ a q n = a + a q + a q 2 + a q 3 + . . . + a q n + . . . ( a ≠ 0 ) \sum_{n=0}^{\infin} aq^n = a+aq+aq^2+aq^3+...+aq^n+...(a\neq0)
n = 0 ∑ ∞ a q n = a + a q + a q 2 + a q 3 + . . . + a q n + . . . ( a = 0 )
|q|<1时,级数收敛;|q|$\geqslant$1时,级数发散。
P级数
∑ n = 1 ∞ 1 n p \sum_{n=1}^{\infin} \frac{1}{n^p}
n = 1 ∑ ∞ n p 1
p>1,级数收敛;p$\leqslant$1级数发散
正项级数的审敛法
比较判别法
lim n → ∞ U n V n = l \lim_{n\rightarrow \infin}\frac{U_n}{V_n}=l
n → ∞ lim V n U n = l
l l l U n , V n U_n,V_n U n , V n
比值判别法
lim n → ∞ U n + 1 U n = l \lim_{n \rightarrow \infin}\frac{U_{n+1}}{U_{n}}=l
n → ∞ lim U n U n + 1 = l
l > 1 l>1 l > 1 l < 1 l<1 l < 1 l = 1 l=1 l = 1
任意项级数的审敛法
幂级数的收敛域
lim n → ∞ ∣ U n + 1 ∣ ∣ U n ∣ = l \lim_{n\rightarrow \infin}\frac{|U_{n+1}|}{|U_n|}=l
n → ∞ lim ∣ U n ∣ ∣ U n + 1 ∣ = l
则函数的收敛半径为r = 1 l r=\frac{1}{l} r = l 1 ( − r , r ) (-r,r) ( − r , r )
无穷级数的加减乘除
参加运算的无穷级数
结果
收敛的无穷级数+ − × / +-\times / + − × /
收敛
收敛的无穷级数+ − × / +- \times / + − × /
发散
发散的无穷级数+ − × / +-\times / + − × /
不一定(改用其它判断方法)
函数展开成幂级数
泰勒公式
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) + o [ ( x − x 0 ) n ] f(x)=f(x_0)+\frac{f^{'}(x_0)}{1!}(x-x_0)+\frac{f^{''}(x_0)}{2!}(x-x_0)+...+\frac{f^{(n)}(x0)}{n!}(x-x_0)+o[(x-x_0)^n]
f ( x ) = f ( x 0 ) + 1 ! f ′ ( x 0 ) ( x − x 0 ) + 2 ! f ′ ′ ( x 0 ) ( x − x 0 ) + . . . + n ! f ( n ) ( x 0 ) ( x − x 0 ) + o [ ( x − x 0 ) n ]
麦克劳林公式
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + . . . + f ( n ) ( 0 ) n ! x n + o ( x n ) f(x)=f(0)+f^{'}(0)x+\frac{f^{''}(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+o(x^n)
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + 2 ! f ′ ′ ( 0 ) x 2 + . . . + n ! f ( n ) ( 0 ) x n + o ( x n )
常用函数展开成x x x
sin x = 1 1 ! x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 + . . . ( − 1 ) n 1 ( 2 n − 1 ) ! x 2 n − 1 + . . . \sin x=\frac{1}{1!}x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+...(-1)^{n}\frac{1}{(2n-1)!}x^{2n-1}+...
sin x = 1 ! 1 x − 3 ! 1 x 3 + 5 ! 1 x 5 − 7 ! 1 x 7 + . . . ( − 1 ) n ( 2 n − 1 ) ! 1 x 2 n − 1 + . . .
e x = 1 + 1 1 ! x + 1 2 ! x 2 + 1 3 ! x 3 + . . . + 1 n ! x n + . . . e^x=1+\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...+\frac{1}{n!}x^n+...
e x = 1 + 1 ! 1 x + 2 ! 1 x 2 + 3 ! 1 x 3 + . . . + n ! 1 x n + . . .
1 1 − x = 1 + x 1 + x 2 + x 3 + x 4 + . . . + x n + . . . \frac{1}{1-x}=1+x^1+x^2+x^3+x^4+...+x^n+...
1 − x 1 = 1 + x 1 + x 2 + x 3 + x 4 + . . . + x n + . . .
平抛运动
点火公式(华里士公式)
\int^{\frac{\pi}{2}}_0\sin^nxdx=\int^{\frac{\pi}{2}}_0\cos^nxdx=
\left\{
\begin{align}
\frac{n-1}{n}&\times \frac{n-3}{n-2}\times...\times\frac{2}{3}\times1 \quad n \space is \space odd\\
\frac{n-1}{n}&\times \frac{n-3}{n-2}\times...\times\frac{1}{2}\times\frac{\pi}{2} \quad n\space is \space even
\end{align}
\right.
二倍角公式
十字相乘
( x + p ) ( x + q ) = x 2 + ( p + q ) x + p q (x+ p)(x+ q)=x^2+(p+q)x+pq
( x + p ) ( x + q ) = x 2 + ( p + q ) x + p q
线性代数公式
∣ A ∣ ∣ B ∣ = ∣ A B ∣ |A||B|=|AB|
∣ A ∣ ∣ B ∣ = ∣ A B ∣
A A ∗ = ∣ A ∣ E AA^*=|A|E
A A ∗ = ∣ A ∣ E
A − 1 = A ∗ ∣ A ∣ A^{-1}=\frac{A^*}{|A|}
A − 1 = ∣ A ∣ A ∗
A × A − 1 = E ∣ A ∣ ∣ A − 1 ∣ = E ∣ A − 1 ∣ = 1 ∣ A ∣ A\times A^{-1}=E\\
|A||A^{-1}|=E\\
|A^{-1}|=\frac{1}{|A|}
A × A − 1 = E ∣ A ∣ ∣ A − 1 ∣ = E ∣ A − 1 ∣ = ∣ A ∣ 1
( A B ) T = B T A T (AB)^T=B^TA^T
( A B ) T = B T A T
( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1}
( A B ) − 1 = B − 1 A − 1
行列式的某行(列)和它代数余子式的乘积之和就是行列式的值(行列式按某行(列)展开定理)
补充:行列式的某行(列)和其他行(列)的代数余子式的乘积之和为0
球体
表面积
S = 4 π r 2 S=4\pi r^2
S = 4 π r 2
体积
V = 4 3 π r 3 V=\frac{4}{3}\pi r^3
V = 3 4 π r 3
圆锥
体积
V = 1 3 π r 2 h V=\frac{1}{3}\pi r^2h
V = 3 1 π r 2 h
扇形
面积
1/2×弧长×半径
n π r 2 / 36 0 。 ( n 为圆心角 ) n\pi r^2 / 360^。 (n\text{为圆心角}) n π r 2 / 3 6 0 。 ( n 为圆心角 )
弧长
2 π r ∗ 角度值 / 360 2\pi r *\text{角度值}/360 2 π r ∗ 角度值 / 3 6 0
三角函数两角和差公式
S i n ( A + B ) = S i n A ∗ C o s B + S i n B ∗ C o s A S i n ( A − B ) = S i n A ∗ C o s B − S i n B ∗ C o s A C o s ( A + B ) = C o s A ∗ C o s B − S i n A ∗ S i n B C o s ( A − B ) = C o s A ∗ C o s B + S i n A ∗ S i n B T a n ( A + B ) = ( T a n A + T a n B ) / ( 1 − T a n A ∗ T a n B ) T a n ( A − B ) = ( T a n A − T a n B ) / ( 1 + T a n A ∗ T a n B ) Sin(A+B)=SinA*CosB+SinB*CosA\\
Sin(A-B)=SinA*CosB-SinB*CosA\\
Cos(A+B)=CosA*CosB-SinA*SinB\\
Cos(A-B)=CosA*CosB+SinA*SinB\\
Tan(A+B)=(TanA+TanB)/(1-TanA*TanB)\\
Tan(A-B)=(TanA-TanB)/(1+TanA*TanB)\\
S i n ( A + B ) = S i n A ∗ C o s B + S i n B ∗ C o s A S i n ( A − B ) = S i n A ∗ C o s B − S i n B ∗ C o s A C o s ( A + B ) = C o s A ∗ C o s B − S i n A ∗ S i n B C o s ( A − B ) = C o s A ∗ C o s B + S i n A ∗ S i n B T a n ( A + B ) = ( T a n A + T a n B ) / ( 1 − T a n A ∗ T a n B ) T a n ( A − B ) = ( T a n A − T a n B ) / ( 1 + T a n A ∗ T a n B )
三角函数和差化积公式及推导
和差化积公式:
sin α + sin β = 2 sin ( α + β 2 ) cos ( α − β 2 ) sin α − sin β = 2 cos ( α + β 2 ) sin ( α − β 2 ) cos α + cos β = 2 cos ( α + β 2 ) cos ( α − β 2 ) cos α − cos β = − 2 sin ( α + β 2 ) sin ( α − β 2 ) \sin \alpha + \sin \beta = 2\sin(\frac{\alpha + \beta}{2})\cos(\frac{\alpha -\beta}{2}) \\
\sin \alpha - \sin \beta = 2\cos(\frac{\alpha + \beta}{2})\sin(\frac{\alpha - \beta}{2}) \\
\cos \alpha + \cos \beta = 2\cos(\frac{\alpha + \beta}{2})\cos(\frac{\alpha - \beta}{2}) \\
\cos \alpha - \cos \beta = -2\sin(\frac{\alpha + \beta}{2})\sin(\frac{\alpha - \beta}{2})
sin α + sin β = 2 sin ( 2 α + β ) cos ( 2 α − β ) sin α − sin β = 2 cos ( 2 α + β ) sin ( 2 α − β ) cos α + cos β = 2 cos ( 2 α + β ) cos ( 2 α − β ) cos α − cos β = − 2 sin ( 2 α + β ) sin ( 2 α − β )
正加正,正在前;
正减正,余在前;
余加余,余并肩;
余减余,负正弦。
三角函数积化和差公式
sin α cos β = sin ( α + β ) + sin ( α − β ) 2 cos α sin β = sin ( α + β ) − sin ( α − β ) 2 cos α cos β = cos ( α + β ) + cos ( α − β ) 2 sin α sin β = − cos ( α + β ) − cos ( α − β ) 2 \sin \alpha \cos \beta = \frac{\sin (\alpha + \beta)+\sin(\alpha-\beta)}{2}\\
\cos\alpha\sin\beta=\frac{\sin (\alpha + \beta)-\sin(\alpha-\beta)}{2}\\
\cos\alpha\cos\beta=\frac{\cos (\alpha + \beta)+\cos(\alpha-\beta)}{2}\\
\sin\alpha\sin\beta=-\frac{\cos (\alpha + \beta)-\cos(\alpha-\beta)}{2}
sin α cos β = 2 sin ( α + β ) + sin ( α − β ) cos α sin β = 2 sin ( α + β ) − sin ( α − β ) cos α cos β = 2 cos ( α + β ) + cos ( α − β ) sin α sin β = − 2 cos ( α + β ) − cos ( α − β )
正余余正,正加正减;
余余正正,余加负余减。
三角函数降幂公式
推导:
直接运用二倍角公式升幂,将该公式变形后可得到降幂公式:
三角函数升幂公式
推导:
将二倍角公式中的2x换成x,相应的x换成x/2就得到升幂公式
三角函数二倍角公式
tan 2 α = 2 tan α 1 − tan 2 α \tan2\alpha=\frac{2\tan \alpha}{1-\tan^2\alpha}
tan 2 α = 1 − tan 2 α 2 tan α
二项式展开定理
组合数采取美式记法( n m ) \tbinom{n}{m} ( m n ) C n m C_{n}^{m} C n m
组合数的计算公式:
C n m = n ! m ! ( n − m ) ! C_{n}^{m}=\frac{n!}{m!(n-m)!}
C n m = m ! ( n − m ) ! n !
极限必须要左右计算的五种类型
a^n-b^n因式分解公式
\begin{align}
a^n-b^n&=(a-b)\sum^{n-1}_{i=0}a^ib^{n-1-i}\\
&=(a-b)(b^{n-1}+ab^{n-2}+a^2b^{n-3}+...+a^{n-3}b^2+a^{n-2}b+a^{n-1})\\
&=(a-b)(a^0b^{n-1}+a^1b^{n-2}+...+a^{n-2}b^1+a^{n-1}b^0)
\end{align}
对数的运算法则
三角函数诱导公式
奇变偶不变,符号看象限
各个象限中各三角函数的正负值:
一全正,二正弦,三正切,四余弦
一元三次方程的解法
猜根法(试出一个根)+长除法(即多项式除法)
例如:因式分解x 3 − 1 x^3-1 x 3 − 1
运用猜根法得到x x x x 3 − 1 x^3-1 x 3 − 1 x − 1 x-1 x − 1
运用长除法得到与x − 1 x-1 x − 1
x 2 − x + 1 x + 1 ) x 3 + 1 ‾ x 3 + x 2 ‾ − x 2 + 1 − x 2 − x ‾ x + 1 x + 1 ‾ 0 \begin{array}{lr}
& x^2-x+1 \\
x+1 \!\!\!\!\!\! & \overline{)x^3 + 1} \\
& \underline{x^3+x^2} \\
& -x^2 + 1 \\
& \underline{-x^2-x} \\
& x+1 \\
& \underline{x+1} \\
& 0 \end{array}
x + 1 x 2 − x + 1 ) x 3 + 1 x 3 + x 2 − x 2 + 1 − x 2 − x x + 1 x + 1 0
待解的一元三次方程是立方差、立方和的形式,可以应用完全立方公式简便的求解
立方差公式
a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a^3-b^3=(a-b)(a^2+ab+b^2)
a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 )
立方和公式
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) a^3+b^3=(a+b)(a^2-ab+b^2)
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 )
和的立方
( a + b ) 3 = a 3 + 3 a 2 b + 3 b 2 a + b 3 (a+b)^3=a^3+3a^2b+3b^2a+b^3
( a + b ) 3 = a 3 + 3 a 2 b + 3 b 2 a + b 3
差的立方
( a − b ) 3 = a 3 − 3 a 2 b + 3 b 2 a − b 3 (a-b)^3=a^3-3a^2b+3b^2a-b^3
( a − b ) 3 = a 3 − 3 a 2 b + 3 b 2 a − b 3
弧度制与角度制的换算公式
1 。 = π 180 1^\text{。}=\frac{\pi}{180} 1 。 = 1 8 0 π π \pi π
1 = ( 180 π ) 。 1=(\frac{180}{\pi})^\text{。} 1 = ( π 1 8 0 ) 。 π \pi π
例如:计算0.2弧度的对应角度值
0.2 × 180 π ≈ 11.465 0.2\times \frac{180}{\pi} \approx 11.465
0 . 2 × π 1 8 0 ≈ 1 1 . 4 6 5
行列式怎么求导
对一个行列式求导,就是对这个行列式的每一行(列)分别求导 ,相加起来就可以了。
周期函数的最小正周期求法
记住周期函数的几个定理即可:
若f ( x ) f(x) f ( x ) M M M T T T K f ( X ) + C ( K ≠ 0 ) K f(X)+C(K≠0) K f ( X ) + C ( K = 0 ) 1 f ( X ) \frac{1}{f(X)} f ( X ) 1 M M M { X / f ( X ) ≠ 0 , X } {X/ f(X) ≠0,X } { X / f ( X ) = 0 , X } T T T
若f ( X ) f(X) f ( X ) M M M T T T f ( a X + b ) f(aX+b) f ( a X + b ) { X ∣ a X + b ∈ M } {X|aX+b\in M } { X ∣ a X + b ∈ M } T a \frac{T}{a} a T
设f ( u ) f(u) f ( u ) M M M u = g ( x ) u=g(x) u = g ( x ) M 1 M_1 M 1 X ∈ M 1 X∈M_1 X ∈ M 1 g ( x ) ∈ M g(x)∈M g ( x ) ∈ M f ( g ( x ) ) f(g(x)) f ( g ( x ) ) M 1 M_1 M 1
设f 1 ( X ) 、 f 2 ( X ) f_1(X)、f_2(X) f 1 ( X ) 、 f 2 ( X ) M M M T 1 、 T 2 T_1\text{、}T_2 T 1 、 T 2 T 1 / T 2 ∈ Q T_1/T_2∈Q T 1 / T 2 ∈ Q M M M T 1 T_1 T 1 T 2 T_2 T 2
设f 1 ( X ) f_1(X) f 1 ( X ) f 2 ( X ) … … f n ( X ) f_2(X)\text{……}f_n(X) f 2 ( X ) … … f n ( X ) M M M T 1 、 T 2 … … T n T_1\text{、}T_2\text{……}T_n T 1 、 T 2 … … T n T 1 , T 2 … … T n T_1\text{,}T_2\text{……}T_n T 1 , T 2 … … T n n n n M M M
sin(arcsecx)=?
令a r c s e c x = t arcsecx = t a r c s e c x = t = sin t =\sin t = sin t
由a r c s e c x = t , sec t = x , arcsecx = t\text{,}\sec t = x\text{,} a r c s e c x = t , sec t = x ,
得出结果sin t = x 2 − 1 x \sin t = \frac{\sqrt{x^2-1}}{x} sin t = x x 2 − 1
数学集合符号
数学集合符号如下:
1、N:非负整数集合或自然数集合{0,1,2,3,…}
2、N*或N+:正整数集合{1,2,3,…}
3、Z:整数集合{…,-1,0,1,…}
4、Q:有理数集合
5、Q+:正有理数集合
6、Q-:负有理数集合
7、R:实数集合(包括有理数和无理数)
8、R+:正实数集合
9、R-:负实数集合
10、C:复数集合
11、∅ :空集(不含有任何元素的集合)
等比数列求和公式
S n = a 1 ( 1 − q n ) 1 − q S_n=\frac{a_1(1-q^n)}{1-q}
S n = 1 − q a 1 ( 1 − q n )
立方和公式
立方和公式是有时在数学运算中需要运用的一个公式。该公式的文字表达为:两数和,乘它们的平方和与它们的积的差,等于这两个数的立方和;表达式为:(a+b)(a²-ab+b²)=a³+b³。